什麼是賽局、奈許均衡?想贏過競爭對手,你該瞭解的經濟學
理論 博弈即是大量的經濟學理論學堆積而成的公式
S8娛樂城十年經營穩定的現金娛樂城手機電腦平板皆可玩
有人當作賭博 有人當作投資 但如果不冒險什麼也得不到
富貴險中求 博弈項目可讓你致富也伴隨風險
現金板不借金 有錢就進來博一場夢想 超過5700倍的獲利等著你
我們提供一個10年信用完美的平台 讓您無後顧之憂
免費註冊!妹子客服可詢問任何相關問題為您解答!請加line:s99s99
註冊網址:http://s888f.top/
附設vip鑽石群 帶你玩百家 六合彩 體育投注
*每年舉辦LA賭城團 鑽石群百家21點勝率最高之15名玩家機酒免費*
*舉辦體育投注神預測之玩家投票,誰能勇奪預測王?*
新手教學網址 https://super888super.blogspot.com
24小時最親切的客服人員服務 ,WebATM及網路購點超迅速,各大超商代碼儲值繳費真方便
暢快百家樂博賞金 連贏挑戰賽非贏不可 二十萬大獎等你拿
贏家祝您財運滾滾來 在家玩樂也可輕鬆大發遊戲財
『s8娛樂城』經營穩定的現金娛樂城
🎉新會員註冊儲值加碼送500,超商儲值便利,趕緊一起同樂
我們有群組歡迎新會員一起聊天交流參與討論哦
【體育賽事】大球賽事通通有~
【六合彩】2星75元,3星65元,4星60元
【今彩539】2星74.3元,3星63.5元,4星57元
【賓果賓果】超級玩法!!5分鐘開一盤,對照台彩!!
【電子遊戲】自創猴子爬樹,捕魚機等多達20款以上!
【真人視訊】百家樂,骰寶,21點,輪盤等應有盡有!!
《經理人月刊》第160期雜誌(本文出自《經理人月刊》2018 年 3 月號,特別企畫:影響世界的 13 堂諾貝爾經濟學課)秦末群雄並起,初掌楚軍兵權的項羽奉命領 5 萬軍,馳赴被秦軍包圍的鉅鹿城救援。面對 30 萬秦軍,項羽渡黃河後,下令將所有船鑿沉,鍋釜也全部打破,讓全營士兵抱著必死的決心作戰。秦將王黎嘲笑項羽,連兵法都不懂,打仗豈能不留後路?沒有想到,楚軍竟以一當十,九戰九捷,大敗秦軍。項羽是自信於楚軍勇猛嗎?恐怕不是,而是項羽了解,5 萬對 30 萬,對方將領只要採取正規戰,失敗的可能性極小,換句話說,想要求勝,只能出其不意。 所以他自斷後路,示敵以弱,讓對手掉以輕心。這種預測局勢得失,布局以牽制對手,進而求勝的思考方式,近似於經濟學中的「賽局理論」。賽局理論最有名的例子,就是普林斯頓大學數學教授阿爾伯特.塔克(Albert Tucker)講解的「囚犯困境」(Prisoner’s Dilemma)。假設警察抓到兩名搶銀行的嫌犯,卻苦無證據定罪。警察將兩人分開囚禁,並分別跟他們說:「如果你不認罪,另一個人認罪,那他會無罪釋放,你唯一死刑。」此案中,嫌犯都清楚,如果彼此都不認罪,頂多證據不足關一年。然而,兩位嫌犯都害怕對方會招認,所以雙雙認罪,而被判 30 年徒刑。囚犯困境指的就是雙方合作(不認罪)可以有更好的結果(關一年),卻因為無法合作而選擇對個人來說最好的條件(認罪頂多關 30 年,比死刑更好)。銀行搶犯的例子,可以幫助我們理解 1994 年諾貝爾經濟學獎得主約翰.奈許(John Nash)所提出的「奈許均衡」(Nash Equilibrium),也叫「非合作均衡」。奈許均衡:單獨一方改變策略時,無法提高報酬
犯人決定要不要認罪,屬於主觀判斷的賽局;若是像隨機出拳的剪刀、石頭、布,長期下來,每種拳出現的機率為 1/3,這種賽局的策略接近客觀機率。當賽局裡這兩種狀況都有可能出現時,就稱為混和策略。奈許證明了:「如果允許混合策略,則參賽者與策略數目有限的任何不合作賽局,都一定會有奈許均衡存在。」當某個組合是奈許均衡時,任何一個參賽者單獨改變自己的策略,並不會使自己的報酬提高。從前面的故事來說,囚犯困境便是奈許均衡。也是因為有了這個定理,討論均衡才有意義,奈許均衡才成為不合作賽局的理論基礎,獲頒 1994 年諾貝爾經濟學獎。賽局的演進:考量行動順序、資訊透明程度
奈許均衡是建立在參與者同時行動的前提上,也就是靜態賽局。但現實社會中,不論企業或個人決策都有先後之分。另一方面,奈許均衡不一定只有一個。比如《玩命關頭7》中,唐老大與戴克蕭開車互撞。最好的情況是一個活著,另一個死亡,這就得賭誰先膽小偏移車道,所以奈許均衡有兩個:唐老大先偏移,戴克蕭直衝;唐老大直衝,戴克蕭先偏移,參賽者難以預測結果。為了解決這兩個問題,同樣在 1994 年獲頒諾貝爾經濟學獎的賴因哈德.澤爾騰(Reinhard Selten)為賽局引入動態的概念,提出「子賽局完美均衡」(SPNE,Subgame Perfect Nash Equilibrium),也就是思考如果讓對手先採取行動,自己應該如何因應;和如果自己先下一步棋,對手可能會採取什麼行動,統籌所有子賽局的可能性之後再做決策。舉例來說,有家新百貨公司準備進入某市場,舊百貨公司可以選擇維持原價或降價。此時,第一個子賽局,是舊公司觀察到新公司進入市場後的賽局;第二個子賽局,是舊公司觀察到新公司不進入市場後的賽局。從各個子賽局的結果,回推舊公司的最適策略。同時,賽局理論原先假設資訊完全透明,跟現實世界的情況不盡相符。所以,1994 年另一位諾貝爾經濟學獎的約翰.海薩尼(John Harsanyi)為了分析不完全訊息之下的非合作賽局理論,提出「貝氏奈許均衡(Bayesian-Nash equilibrium)」。舉例來說,B 企業考慮進入 A 企業獨佔的某市場。B 企業知道,A 企業是否會阻擾他進入,取決於阻擾所花費的成本:如果成本高,A 就不會阻擾;如果成本低,A 就會阻擾。然而,A 企業的阻擾成本是多少,B 企業卻不知道。這種 A 方知道,B 方卻不知道的資訊,在海薩尼的非合作賽局中被稱為類型(types)。A、B 企業都知道自己的類型(成本高、成本低),不知道另一方的類型,但卻能得知類型的分佈,如阻擾成本高的機率是 60%、阻擾成本低的機率是 40%。貝氏奈許均衡中,參賽者只知道自己的類型,不知道其他人的類型,但所有人都知道類型的分佈。所以,參賽者只能依照自己的類型,與類型的分布,找出利益最大化的決策。從定價策略學賽局理論:優勢策略與奈許均衡
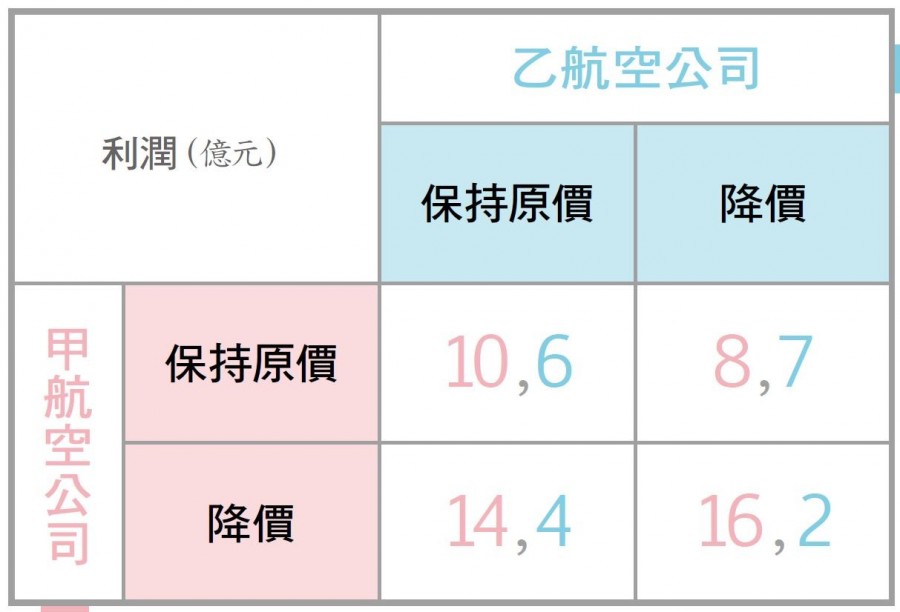
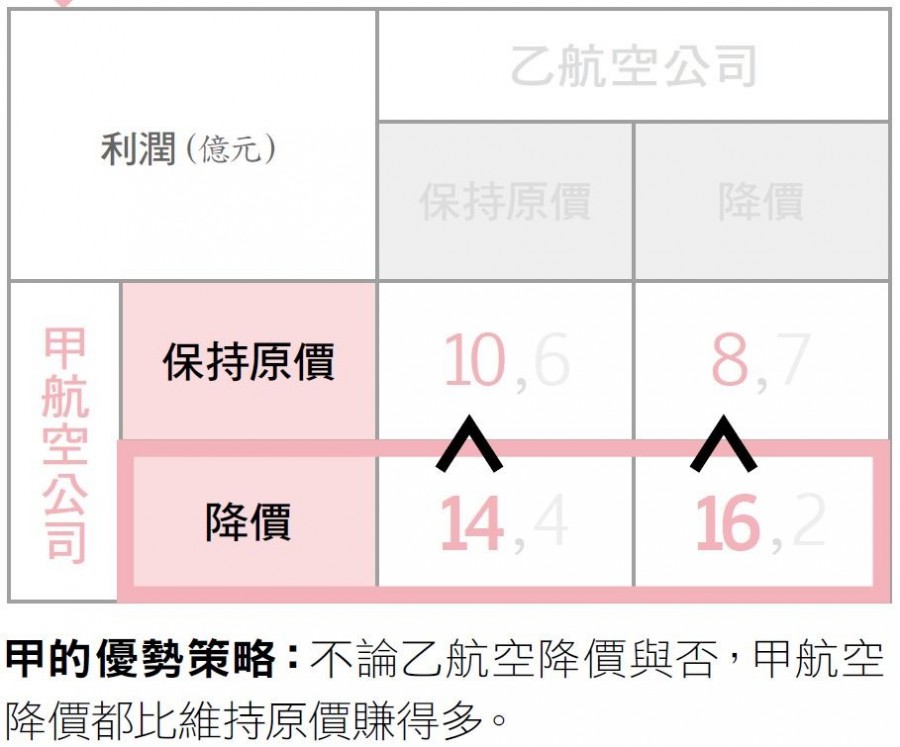
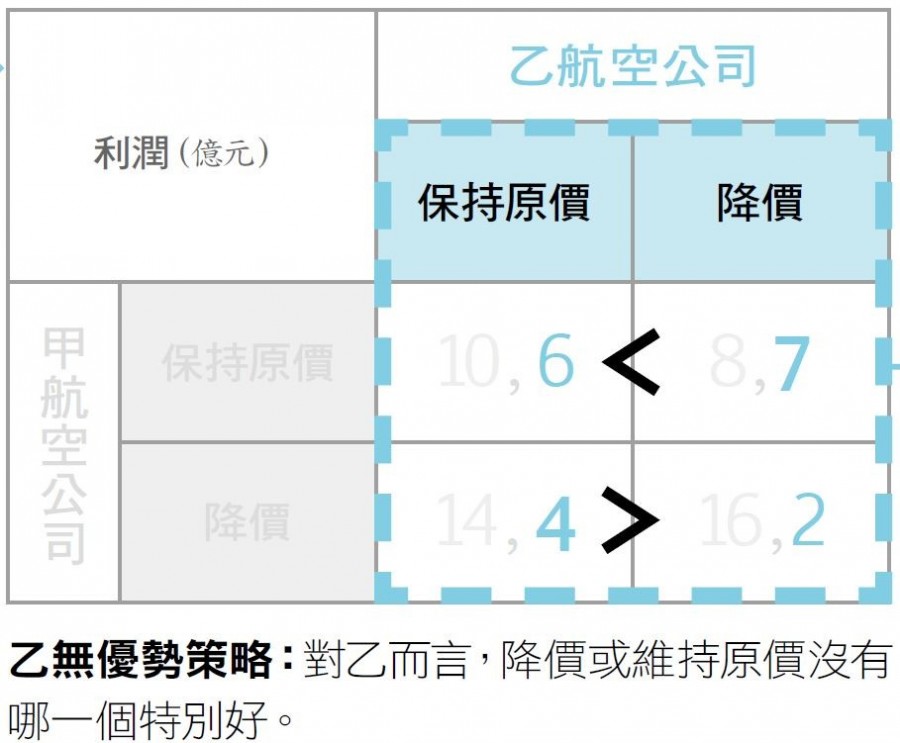
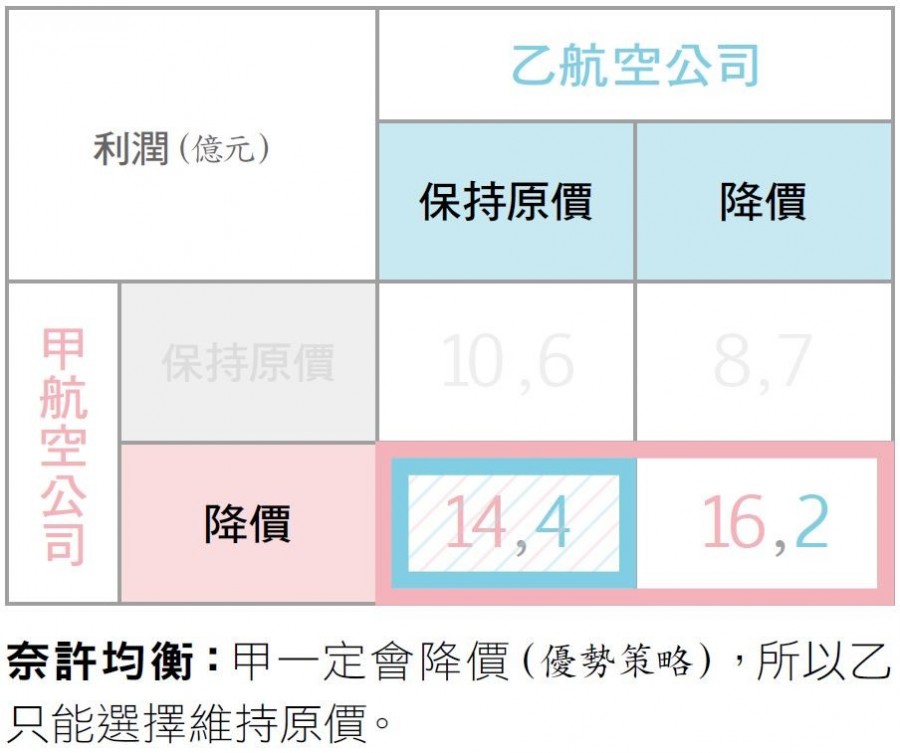
甲乙航空公司的定價賽局。陳姿伶 / 製圖甲、乙兩家相互競爭的航空公司,在上圖標示出兩方選擇原價策略和降價策略後的結果。在決定票價前,企業應該要先探索自己有無「優勢策略」。以下拆解成3張圖來做解讀:當甲、乙都採原價時,甲的利潤有 10 億,乙的利潤有 6 億。但假如甲航空公司通過計算後發現,無論自己降價後因為搶奪乙的市占率,無論乙有沒有降價,都可以得到更多的利潤,因此甲一定會降價。甲的定價策略。陳姿伶 / 製圖乙航空公司完全沒有優勢,降價或維持原價可獲得的利潤,要看甲航空公司的價格策略而定。乙的定價策略。陳姿伶 / 製圖因此在甲航空公司選擇降價後,乙航空公司只能依此選擇維持原價。兩家價格調整後的奈許均衡。
沒有留言:
張貼留言